
Статью подготовили специалисты образовательного сервиса Zaochnik.
Механические волны
Содержание:
Когда в каком-нибудь месте твердой, жидкой или газообразной среды происходит возбуждение колебаний частиц, результатом взаимодействия атомов и молекул среды становится передача колебаний от одной точки к другой с конечной скоростью.
Волна – это процесс распространения колебаний в среде.
Виды механических волн
Различают следующие виды механических волн:
Поперечная волна: частицы среды смещаются в направлении, перпендикулярном направлению распространения механической волны.
Пример: волны, распространяющиеся по струне или резиновому жгуту в натяжении (рисунок );
Продольная волна: частицы среды смещаются в направлении распространения механической волны.
Пример: волны, распространяющиеся в газе или упругом стержне (рисунок ).
Интересно, что волны на поверхности жидкости включают в себя и поперечную, и продольную компоненты.
Укажем важное уточнение: когда механические волны распространяются, они переносят энергию, форму, но не переносят массу, т.е. в обоих видах волн переноса вещества в направлении распространения волны не происходит. Распространяясь, частицы среды совершают колебания около положений равновесия. При этом, как мы уже сказали, волны переносят энергию, а именно энергию колебаний от одной точки среды к другой.
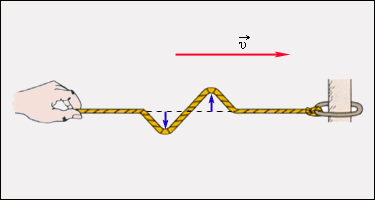
Рисунок Распространение поперечной волны по резиновому жгуту в натяжении.
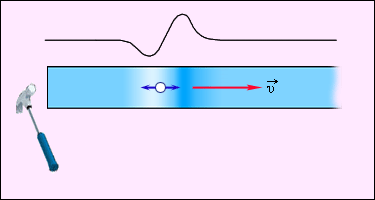
Рисунок Распространение продольной волны по упругому стержню.
Модель твердого тела
Характерная черта механических волн – их распространение в материальных средах в отличие, например, от световых волн, способных распространяться и в пустоте. Для возникновения механического волнового импульса необходима среда, имеющая возможность запасать кинетическую и потенциальную энергии: т.е. среда должна иметь инертные и упругие свойства. В реальных средах эти свойства получают распределение по всему объему. К примеру, каждому небольшому элементу твердого тела присуща масса и упругость. Самая простая одномерная модель такого тела представляет из себя совокупность шариков и пружинок (рисунок ).
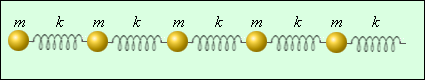
Рисунок Простейшая одномерная модель твердого тела.
В этой модели инертные и упругие свойства разделены. Шарики имеют массу , а пружинки – жесткость . Такая простая модель дает возможность описать распространение продольных и поперечных механических волн в твердом теле. При распространении продольной волны шарики смещаются вдоль цепочки, а пружинки растягиваются или сжимаются, что есть деформация растяжения или сжатия. Если подобная деформация происходит в жидкой или газообразной среде, ее сопровождает уплотнение или разрежение.
Отличительная особенность продольных волн заключается в том, что они способны распространяться в любых средах: твердых, жидких и газообразных.
Если в указанной модели твердого тела один или несколько шариков получают смещение перпендикулярно всей цепочке, можно говорить о возникновении деформации сдвига. Пружины, получившие деформацию в результате смещения, будут стремиться вернуть смещенные частицы в положение равновесия, а на ближайшие несмещенные частицы начнет оказываться влияние упругих сил, стремящихся отклонить эти частицы от положения равновесия. Итогом станет возникновение поперечной волны в направлении вдоль цепочки.
В жидкой или газообразной среде упругая деформация сдвига не возникает. Смещение одного слоя жидкости или газа на некоторое расстояние относительно соседнего слоя не приведет к появлению касательных сил на границе между слоями. Силы, которые оказывают воздействие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. Аналогично можно сказать и о газообразной среде.
Таким образом, появление поперечных волн невозможно в жидкой или газообразной средах.
В плане практического применения особый интерес представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой колебания частиц, частотой и длиной волны . Синусоидальные волны получают распространение в однородных средах с некоторой постоянной скоростью .
Запишем выражение, показывающее зависимость смещения частиц среды из положения равновесия в синусоидальной волне от координаты на оси , вдоль которой распространяется волна, и от времени :
.
В приведенном выражении – так называемое волновое число, а является круговой частотой.
Бегущая волна
Рисунок демонстрирует «моментальные фотографии» поперечной волны в момент времени и . За промежуток времени волна перемещается вдоль оси на расстояние . Подобные волны носят название бегущих волн.
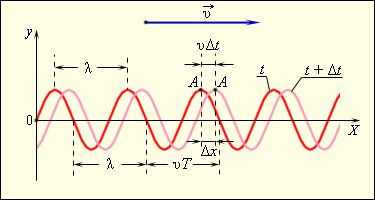
Рисунок «Моментальные фотографии» бегущей синусоидальной волны в момент времени и .
Длина волны – это расстояние между двумя соседними точками на оси , испытывающими колебание в одинаковых фазах.
Расстояние, величина которого есть длина волны , волна проходит за период . Таким образом, формула длины волны имеет вид: , где является скоростью распространения волны.
С течением времени происходит изменение координаты любой точки на графике, отображающем волновой процесс (к примеру, точка на рисунке ), при этом значение выражения остается неизменным. Спустя время точка переместится по оси на некоторое расстояние . Таким образом:
или .
Из указанного выражения следует:
или .
Становится очевидно, что бегущая синусоидальная волна имеет двойную периодичность – во времени и пространстве. Временной период является равным периоду колебаний частиц среды, а пространственный период равен длине волны .
Волновое число – это пространственный аналог круговой частоты .
Сделаем акцент на том, что уравнение является описанием синусоидальной волны, получающей распространение в направлении, противоположном направлению оси , со скоростью .
Когда бегущая волна получает распространение, все частицы среды гармонически колеблются с некоторой частотой . Это означает, что как и при простом колебательном процессе, средняя потенциальная энергия, являющаяся запасом некоторого объема среды, есть средняя кинетическая энергия в том же объеме, пропорциональная квадрату амплитуды колебаний.
Из вышесказанного можно сделать вывод, что, когда бегущая волна получает распространение, появляется поток энергии, пропорциональный скорости волны и квадрату ее амплитуды.
Скорость распространения волны
Бегущие волны движутся в среде с определенными скоростями, находящимися в зависимости от типа волны, инертных и упругих свойств среды.
Скорость, с которой поперечные волны распространяются в натянутой струне или резиновом жгуте, имеет зависимость от погонной массы (или массы единицы длины) и силы натяжения :
.
Скорость, с которой продольные волны распространяются в безграничной среде, рассчитывается при участии таких величин как плотность среды (или масса единицы объема) и модуль всестороннего сжатия (равен коэффициенту пропорциональности между изменением давления и относительным изменением объема , взятому с обратным знаком):
.
Таким образом, скорость распространения продольных волн в безграничной среде, определяется по формуле:
.
При температуре скорость распространения продольных волн в воде , в различных сортах стали .
Если речь идет о продольных волнах, получающих распространение в упругих стержнях, запись формулы для скорости волны содержит не модуль всестороннего сжатия, а модуль Юнга:
.
Для стали отличие от незначительно, а вот для прочих материалов оно может составлять и больше.
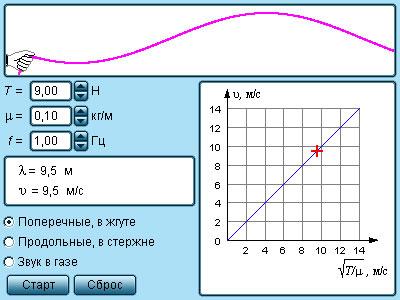
Рисунок Модель продольных и поперечных волн.
Стоячая волна
Предположим, что механическая волна, получившая распространение в некоторой среде, встретила на пути некое препятствие: в этом случае характер ее поведения резко изменится. К примеру, на границе раздела двух сред с различающимися механическими свойствами волна частично отразится, а частично проникнет во вторую среду. Волна, пробегающая по резиновому жгуту или струне, отразится от зафиксированного конца, и возникнет встречная волна. Если у струны зафиксированы оба конца, появятся сложные колебания, являющиеся итогом наложения (суперпозиции) двух волн, получающих распространение в противоположных направлениях и испытывающих отражения и переотражения на концах. Так «работают» струны всех струнных музыкальных инструментов, зафиксированные с обоих концов. Схожий процесс возникает при звучании духовых инструментов, в частности, органных труб.
Если волны, распространяющиеся по струне во встречных направлениях, обладают синусоидальной формой, то при определенных условиях они образуют стоячую волну.
Допустим, струна длины зафиксирована таким образом, что один из ее концов расположен в точке , а другой – в точке (рисунок ). В струне имеется натяжение .
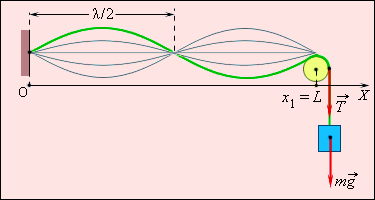
Рисунок Возникновение стоячей волны в струне, зафиксированной на обоих концах.
По струне одновременно пробегают в противоположных направлениях две волны с одинаковой частотой:
- – волна, распространяющаяся справа налево;
- – волна, распространяющаяся слева направо.
Точка - один из зафиксированных концов струны: в этой точке падающая волна в результате отражения создает волну . Отражаясь от зафиксированного конца, отраженная волна входит в противофазу с падающей. В соответствии с принципом суперпозиции (что есть экспериментальный факт) колебания, созданные встречными волнами во всех точках струны, суммируются. Из сказанного следует, что итоговое колебание в каждой точке определяется как сумма колебаний, вызванных волнами и в отдельности. Таким образом:
.
Приведенное выражение является описанием стоячей волны. Введем некоторые понятия, применимые к такому явлению как стоячая волна.
Узлы – точки неподвижности в стоячей волне.
Пучности – точки, расположенные между узлами и колеблющиеся с максимальной амплитудой.
Если следовать данным определениям, для возникновения стоячей волны оба зафиксированных конца струны должны являться узлами. Указанная ранее формула отвечает этому условию на левом конце . Чтобы условие было выполнено и на правом конце , необходимо чтобы , где является любым целым числом. Из сказанного можно сделать вывод, что стоячая волна в струне появляется не всегда, а только тогда, когда длина струны равна целому числу длин полуволн:
или .
Набору значений длин волн соответствует набор возможных частот
.
В этой записи есть скорость, с которой распространяются поперечные волны по струне.
Каждая из частот и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота носит название основной частоты, все прочие называются гармониками.
Рисунок иллюстрирует нормальную моду для .
Стоячая волна не обладает потоком энергии. Энергия колебаний, «запертая» в отрезке струны между двумя соседними узлами, не переносится в остальные части струны. В каждом таком отрезке происходит периодическое (дважды за период ) преобразование кинетической энергии в потенциальную и обратно, подобно обычной колебательной системе. Однако, здесь имеется различие: если груз на пружине или маятник имеют единственную собственную частоту , то струна характеризуется наличием бесконечного числа собственных (резонансных) частот . На рисунке показано несколько вариантов стоячих волн в струне, зафиксированной на обоих концах.
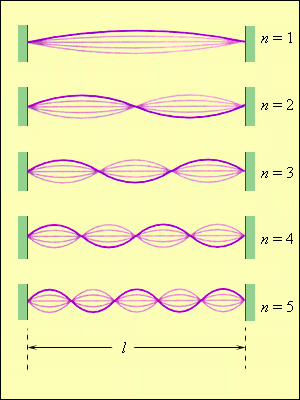
Рисунок Первые пять нормальных мод колебаний струны, зафиксированной на обоих концах.
Согласно принципу суперпозиции стоячие волны различных видов (с разными значениями ) способны одновременно присутствовать в колебаниях струны.
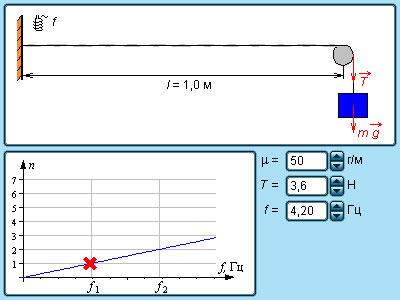
Рисунок Модель нормальных мод струны.
Навигация по статьям
