
Статью подготовили специалисты образовательного сервиса Zaochnik.
Скорость света в однородных изотропных диэлектриках
Содержание:
Разберем распространение ЭМВ, происходящее в однородных изотропных диэлектриках с диэлектрической проницаемостью, не зависящей от координат. Считаем, что она не зависит и от времени. Это говорит о необходимости замены (относительной диэлектрической проницаемости) в уравнениях Максвелла. Выражение определения показывает, чему равна скорость света в фазе:
,
где является коэффициентом (показателем) преломления диэлектрика.
Тогда выражения для длины волны запишется как:
.
Волновое число будет равняться:
.
Выражение связи объемной плотности энергии с плотностью потока энергии запишется как:
.
Скорость света в веществе и в вакууме
В диэлектриках скорость распространения световых ЭМВ находится в зависимости от частоты. Явление получило название дисперсии.
Ее проявление характерно для рассеивания немонохроматических волн, то есть рассылка с различными скоростями ее монохроматических составляющих с различными частотами. Дисперсия считается следствием зависимости атомов от частоты. Чтобы найти явный вид , которая входит в состав материальных уравнений, используют микроскопическую классическую теорию взаимодействия электромагнитного поля волны с веществом. Эта теория следует из определенной идеализированной модели строения вещества.
Модель газообразной среды выделяется наибольшей простотой. Это возможно, так как при первом приближении разрешено исключить учитывание взаимодействия атомов или молекул, а полагать совпадение действующего на отдельный атом поля со средним полем ЭМВ.
Чтобы получить макроскопическое материальное уравнение, следует принять во внимание действие поля ЭМВ на изолированный атом в таких условиях. Использование классической теории требует осторожности. Данный случай указывает на то, что результат квантовой дисперсии будет аналогичен результату классической.
Классическая теория дисперсии указывает на взаимодействие электромагнитного поля с электроном(внешний или оптический электрон), который рассматривается в качестве затухающего дипольного осциллятора, характеризуемого определенной собственной и постоянной затухания . Таким образом, уравнение его движения в поле световой волны запишется как:
,
где является смещением электрона из положения равновесия, и – зарядом и массой электрона. Для нахождения решения следует привести к виду:
.
Результат:
.
Формула дипольного момента атома , индуцированного полем :
.
При , являющейся концентрацией электронов с собственной частотой колебаний , определение поляризованности среды возможно при помощи выражения:
.
Поляризованность (поляризация) среды может быть представлена в виде:
,
где является линейной диэлектрической восприимчивостью среды, зависящей от частоты . При использовании векторов и прослеживается наличие их связи в соотношении:
.
Следовательно, из вытекает:
,
а из получаем:
или .
Имеем, , то показатель преломления и скорость электромагнитной волны находятся в зависимости от частоты. Значение является комплексной величиной:
.
Учитывая , приходим к системе уравнений:
.
Значение для прозрачных или частично прозрачных в оптическом диапазоне диэлектриком очень мало. Следовательно:
и .
Из имеющегося приближения имеем:
.
Если в среде дисперсию определяют различные совокупности электронов, обладающие собственными частотами и имеющие концентрациями , то формула обобщается:
.
Данное выражение не учитывает колебания ионов. Значение их массы намного больше массы электронов, что способствует собственным частотам ионов располагаться в дальней инфракрасной области.
Нормальная дисперсия
Вдали от собственных резонансов величина приближена к (для прозрачных диэлектриков, разреженных газов):
.
Следовательно:
.
Рассмотрим графическую зависимость (дисперсионную кривую), показанную на рисунке .
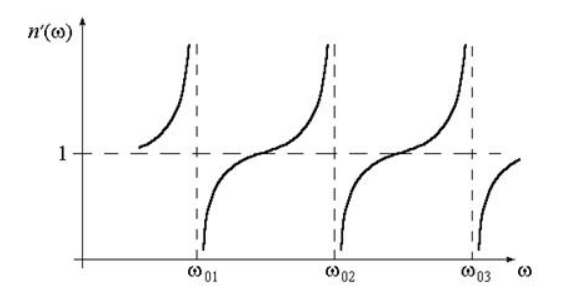
Рисунок
При увеличении действительной части показателя преломления происходит рост частоты, тогда дисперсия получает название нормальной.
Вся область прозрачности диэлектриков служит для наблюдения нормальной дисперсии. Если имеются малые частоты , то указывает на статистическое значение показателя преломления:
.
Возможно, что оно будет заметно отличаться от значения показателя преломления для оптических частот. Например, вода имеет в области оптических частот , а статистическое значение . При условии больших частот и :
.
Следовательно, коротковолновое излучение диэлектрика говорит об оптически менее плотной среде в отличие от вакуума. Наличие рентгеновского излучения характеризуется полным отражением. Если имеются большие частоты, способ связи электронов не имеет значение, а показатель преломления зависит от общей концентрации всех электронов.
Аномальная дисперсия
Если не учитывать затухание , это приведет к при . Но вблизи собственных частот нельзя пренебречь . Отсюда следует, – непрерывная функция. Если разделить на мнимые и вещественные части по формуле , учитывая приближение , получаем:
.
На рисунке показаны дисперсионные кривые .
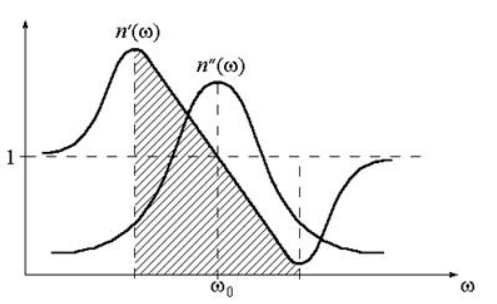
Рисунок
Вблизи резонансной частоты показатель преломления уменьшается с ростом частоты. Явление называют аномальной дисперсией.
Определение величины поглощения происходит через мнимую часть показателя преломления. Вследствие этого область аномальной дисперсии соответствует области поглощения световых волн имеющимся веществом. Это применимо для целей спектроскопии.
Граничные условия
Граничные условия для векторов поля световой волны на разделении между двумя диэлектриками при отсутствии свободных зарядов и токов проводимости имеют вид:
где являются индексами тангенциальной (касательной к границе раздела) и нормальной компоненты вектора соответственно.
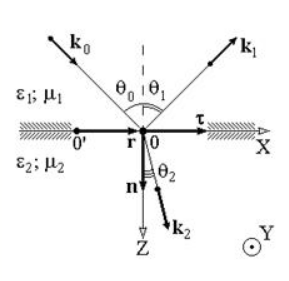
Рисунок
Предположим, что на плоскую границу двух диэлектриков с абсолютными проницаемостями и (вид магнитной проницаемости остается общим) падает под некоторым углом плоская световая волна, изображенная на рисунке . Отсюда получим формулы для напряженностей электрического поля в падающей, отраженной, преломленной волн соответственно:
,
где считаются волновыми числами,
– скоростями света в -й и -й средах.
Законы отражения и преломления света на границе определены граничными условиями . Электрическое поле, учитывающее , приводит к новому виду граничных условий:
.
Началом отсчета является произвольный вектор (точка ). При условии нахождения на поверхности раздела получим:
.
Тогда в :
.
Любая точка поверхности характеризуется равенством , поэтому рекомендовано точку размещать на границе раздела.
Равенство будет соблюдено для произвольных и , если
;
.
Следовательно, при отражении и преломлении не происходит изменение частоты ЭМВ:
.
Выберем точку таким образом, чтобы вектор ( следует направить плоскости перпендикулярно относительно друг друга, как показано на рисунке ). Значит, , а из вытекает, что . Это говорит о том, что волновые векторы падающей, отраженной и преломленной волн располагаются в одной плоскости.
Плоскость, в которой находятся волновой вектор и нормаль к поверхности раздела в точке падения луча, получила название плоскости падения.
По рисунку видно, что
.
Учитывая , имеем:
,
Из :
.
Значения являются показателями преломления. Выражение дает понять, что
Вводим обозначение – относительный показатель преломления .
Приходим к новому виду закона Снеллиуса:
.
Если (падение из менее оптически плотной в более плотную среду), то . Это показано на рисунке Когда , тогда . Подробно изображено на рисунке .
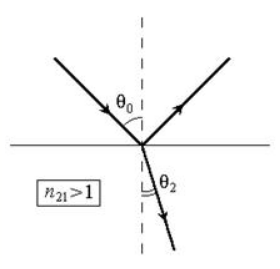
Рисунок
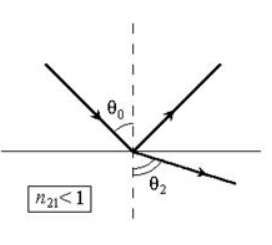
Рисунок
Значение вектора в падающей волне может иметь произвольный азимут , то есть угол, находящийся между и плоскостью падения. Произведем разложение векторов электромагнитного поля на две составляющие являются перпендикулярные плоскости падения, обозначаемые или , и параллельные, которые выделяют в виде или , как показано на рисунке .
.
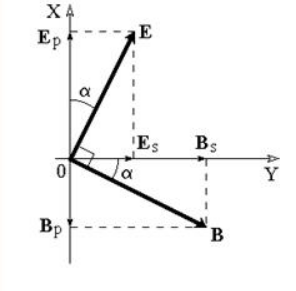
Рисунок
Отсюда видно, что векторы и составляют правовинтовые тройки векторов и сами образуют плоские ЭМВ. Формула говорит о равнении плотности потока энергии исходной волны сумме плотностей потока энергии волн, на которых она раскладывается. То есть разложение плоской волны с произвольным азимутом на сумму волн, у одной из которых ( – поляризация) располагается в плоскости падения, а у другой ( - поляризация) – перпендикулярна ей. После изучения поведения этих волн на границе с учетом принципа суперпозиции и аддитивности плотностей потока энергии получаем поведение ЭМВ с произвольным азимутом.
Отражение и преломление -поляризованный ЭМВ
Такое отражение и преломление изображено на рисунке .
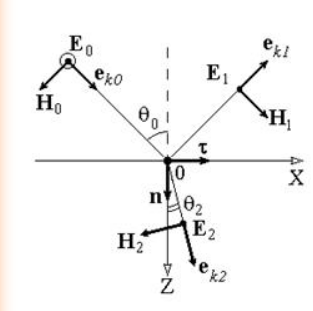
Рисунок
При введении единичных векторов по направлению получим:
.
Само направление векторов и не известно заранее. Сделаем это условно, как показано на рисунке . При наличии отрицательного знака направление векторов идет в противоположную сторону.
Отметим граничные условия для -поляризации с опусканием индексов:
.
Введем обозначение в качестве волнового сопротивления (импеданса) среды. Его же значение для вакуума – . В отличие от электричества, оптика предлагает практически не применять понятие волнового сопротивления среды. Чтобы запись была удобной, ее оставляют в уравнении:
.
По рисунку видна связь :
.
Чтобы использовать далее , получим из скалярное произведение для любой из рассматриваемых волн:
.
Учитывая известные формулы векторного анализа
имеем:
.
Из получим, что:
.
Запись соотношений примет вид:
.
Возьмем обозначение:
амплитудным коэффициентом отражения ;
амплитудным коэффициентом пропускания .
Учитываем:
.
Если система обладает действительными решениями для всех углов . При она характеризуется действительным решением только для углов . Получаем:
.
(Обобщенные формулы Френеля для -поляризации)
Диэлектрики с оптическим диапазоном . Отсюда из выводим общепринятые формулы Френеля для диэлектриков с -поляризацией:
.
На рисунке изображены графики зависимостей и для .
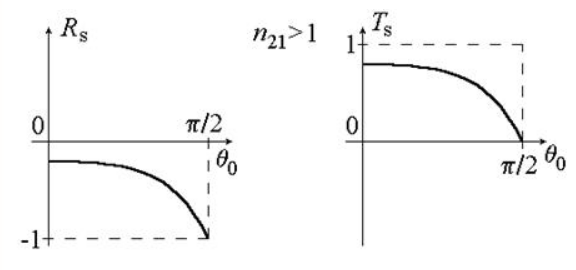
Рисунок
Если свет отражается от диэлектрика с , фаза отраженной волны проходит изменение на . Когда происходит преломление, то фаза отсутствует.
Отражение света от диэлектрика с говорит о том, что не имеется скачка фазы на для отраженной и для преломленной волн ( углы , то есть при полном внутреннем отражении поведение фазы усложняется).
Отражение и преломление -поляризованной ЭМВ
Такое отражение и преломление изображено на рисунке .
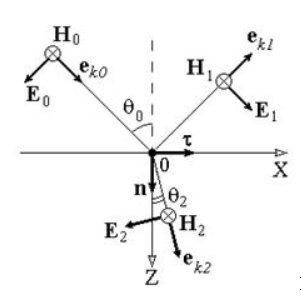
Рисунок
Данное рассмотрение проводится аналогично -поляризации. Поэтому учитываем:
Тогда:
.
Граничные условия -поляризации запишутся как:
Далее произведем подстановку в :
При действительных углах преломления получим обобщенные формулы Френеля для
-поляризации:
или для диэлектриков с :
На рисунке показаны графики зависимостей и для .
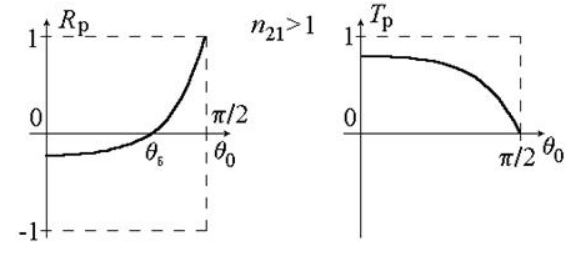
Рисунок
Явление Брюстера
Рассматривая формулы и график, изображенный на рисунке , понятно, что для -поляризованной волны с углом падения , называемом углом Брюстера, отраженная волна отсутствует, то есть . Это получило название явления Брюстера.
Для такого угла считаются справедливыми соотношения:
.
Данное явление можно наблюдать при ортогональном направлении преломленной и отраженной волн. Это объяснимо таким образом: при связывании наличия отраженной волны с вынужденными колебаниями электронов во второй среде и перпендикулярном направлении преломленной волны энергия не должна распространяться, так как образующийся при этом диполь не способен излучать в направлении собственных колебаний.
Во время перехода через угол Брюстера фаза колебаний отраженной волны меняется на в виде скачка. Если , то падающая волна с произвольным азимутом отражается только с -поляризованной компонентой. Это был представлен один из способов получения линейно-поляризованного света.
Стопа Столетова, изображенная на рисунке , при падении света на нее
-компонента волны на каждой поверхности частично отражается, а -компонента проходит полностью. Стопа Столетова состоит из плоскопараллельных стеклянных пластин с наличием воздушного зазора между ними.

Рисунок
На выходе получаем практически линейно-поляризованный свет. Если падение нормальное , понятие и поляризаций утрачивают смысл, а формулы выдают аналогичный результат (для диэлектрика ):
Энергетические соотношения при преломлении и отражении
Энергетический коэффициент отражения – абсолютное значение отношения нормальных компонент векторов Пойнтинга в отраженной и падающей волнах:
.
Введение производится аналогично и для преломленной волны:
,
т.к.
Тогда для получим:
Учитывая , имеем:
Когда для :
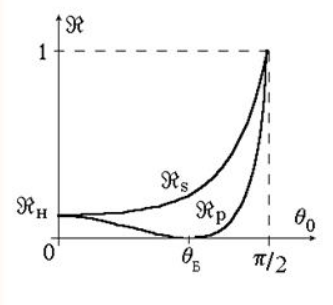
Рисунок
Прямая проверка показывает:
.
Это способствует выражению закона сохранения энергии при отражении и преломлении света на границе раздела двух сред.
На рисунке показаны графики .
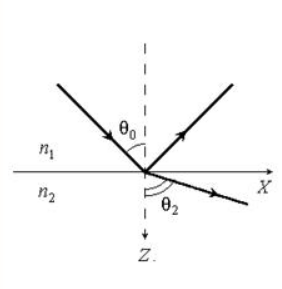
Рисунок
Явление полного внутреннего отражения
При падении света на границу двух диэлектриков, , как показано на рисунке , из закона Снеллиуса следует, что существует предельный (критический) угол падения, при котором угол преломления .
Отсюда:
.
При угол преломления обозначается в качестве обычной геометрической интерпретации, коэффициенты и считаются вещественными.
Если угол падения , то вещественный угол преломления не существует, так как закон Снеллиуса выдает для значение , а для – мнимое значение:
.
Формулы Френеля будут считаться справедливыми только при рассмотрении закона преломления в качестве определения входящих в них величин и , соответствуя выражению . Справедливость формул Френеля, понимаемых в таком ракурсе, идет из обеспечения выполнения граничных условий в данном случае.
При рассмотрении световой волны во второй среде (преломленной) в общем случае, имеем:
.
Данная запись показывает, что первый сомножитель говорит о комплексной амплитуде волны , которая распространяется вдоль , обладающая скоростью . Произведем подстановку в :
.
Положительность первой экспоненты говорит о безграничном возрастании поля в среде, это не имеет смысл. Знак указывает на быстро убывающую с ростом амплитуду волны, которая распространяется во второй среде вдоль . На практике существование такой неоднородной волны возможно в поверхностном слое второй среды толщиной порядка длины волны. Фазовая скорость этой неоднородной волны находится в зависимости от свойств среды, угла падения.
Вид формул Френеля для отраженной волны ( и с ):
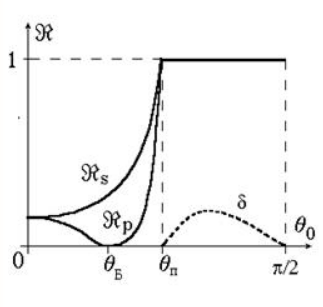
Рисунок
Замечаем значение энергетических коэффициентов при углах падения больше критического, как показано на рисунке . Явление получило название полного внутреннего отражения (ПВО). При прохождении волны с соответствующей долей энергии через границу раздела во вторую среду идет на определенную глубину (глубину проникновения) (амплитуда поля на глубине характеризуется падением в раз), производит движение вдоль поверхности раздела, следует возвращение в первую среду.
.
Места, где энергия входит во вторую среду, а ее возвращение в первую смещается относительно друг друга. Амплитуды и компонент отраженной волны остается без изменений по абсолютному значению, но имеют в наличии различные фазовые сдвиги. После представления
то
Введем обозначения .
Отсюда
.
- Призма-крыша.
- Световоды.
- Миражи.
- Ромб (параллелепипед) Френеля с .
Если рассматривать вопрос применения электромагнитной теории Максвелла для данного случая, то решение задач сводится к учитыванию проводимости металла, иначе говоря, к введению в уравнения Максвелла зависящих от коэффициента электропроводности членов. Отражение света от поверхности металла, распространение рассматривается, основываясь на материальных уравнениях, где диэлектрическая проницаемость является комплексной. Отсюда следует, что показатель преломления является комплексной величиной:
При наличии сильно поглощающих сред и металлов мнимая часть преобладает над вещественной.
Токи проводимости создаются посредствам частичного проникновения света в металл. Это говорит о связи с джоулевой теплотой, то есть с поглощением света – необратимым превращением электромагнитной энергии в энергию беспорядочного теплового движения. Большей проводимости металла соответствует меньшая доля падающего света, проникающего в металл и поглощаемого там. Идеальный проводник, где , говорит об отсутствии потерь джоулевой теплоты, поэтому падающий свет должен быть полностью отражен.
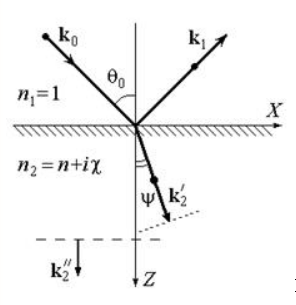
Рисунок
Допустим, из вакуума на металл будет падать плоская монохроматическая волна с вектором , изображенном на рисунке , где является волновым вектором отраженной волны. Вторая среда говорит о неоднородности волны:
.
Чтобы произвести вывод формул Френеля:
.
Замечаем, что составляющая вектора , которая направлена вдоль границы, считается вещественной. Отсюда и перпендикулярность мнимой части вектора к поверхности металла. Следует, что плоскости с равными амплитудами прошедшей волны считаются параллельными относительно границ раздела. Расположение вектора перпендикулярно плоскостям с постоянными фазами и характеризует направление прошедшей волны.
Угол у получил название вещественного угла преломления.
Угол падения (в отличие от диэлектриков) характеризует отношение .
Действенность формул Френеля возможна при рассматривании в качестве комплексной величины:
.
Знак корня служит для затухания неоднородной волны вглубь металла. Следовательно, коэффициенты отражения считаются комплексными:
Общий случай говорит о . Если имеется линейная поляризация падающего света с наличием произвольного азимута в отраженной волне, то происходит появление сдвига фаз, приводящий к эллиптической поляризации отраженного света. Именно он остается линейно поляризованным при условии, что:
- падающий свет или поляризован;
- ;
- .
Если падение нормальное, то:
Значение у металлов больше, чем другие слагаемые. Отсюда , как показано в таблице для желтой части спектра.
Оптические постоянные для металлов
| Металл | |||
Таблица
Волновой вектор, прошедший в металл при нормальном падении, обладает только z-составляющей:
;
– глубина проникновения.
Если частоты довольно высокие, то сила трения в уравнениях колебаний электрона оказывается несущественной. При имеется соответствие с идеальным металлом. Видно:
, а
.
Из имеем , иначе говоря, происходит полное отражение от поверхности идеального проводника.
Закон Бугера
Если затухающая волна распространяется вдоль , ее интенсивность излучения записывается как:
.
Придем к зависимости:
, называемой законом Бугера с линейным показателем поглощения в виде . Иначе данный закон выражается в :
, где обозначается длиной волны в вакууме.
Навигация по статьям
