
Статью подготовили специалисты образовательного сервиса Zaochnik.
Сила и плотность тока. Линии тока
Содержание:
Сила тока для тока, протекающего через некоторую площадь сечения проводника эквивалентна производной заряда q по времени и количественно характеризует электрический ток.
Таким образом выходит, что сила тока — это поток заряженных частиц через некоторую поверхность .
Электрический ток является процессом движения как отрицательных, так и положительных зарядов.
Перенос заряда одного знака в определенную сторону равен переносу заряда, обладающего противоположным знаком, в обратном направлении. В ситуации, когда ток образуется зарядами и положительного, и отрицательного знаков ( и ), справедливым будет заключение о том, что сила тока равна следующему выражению:
.
В качестве положительного определяют направление движения положительных зарядов. Ток может быть постоянным, когда ни сила тока, ни его направление не претерпевают изменений с течением времени, или, наоборот, переменным. При условии постоянства, формула силы тока может выражаться в следующем виде:
,
где сила тока определена в качестве заряда, который пересекает некоторую поверхность в единицу времени. В системе роль основной единицы измерения силы тока играет Ампер .
.
Плотность тока. Связь плотности тока с зарядом и силой тока, напряженностью
Выделим в проводнике, в котором протекает ток, малый объем случайной формы. С помощью следующего обозначения определим среднюю скорость движения носителей зарядов в проводнике. Пускай представляет собой концентрацию носителей заряда. На поверхности проводника выберем пренебрежительно малую площадку , которая расположена ортогонально скорости (рис. ).
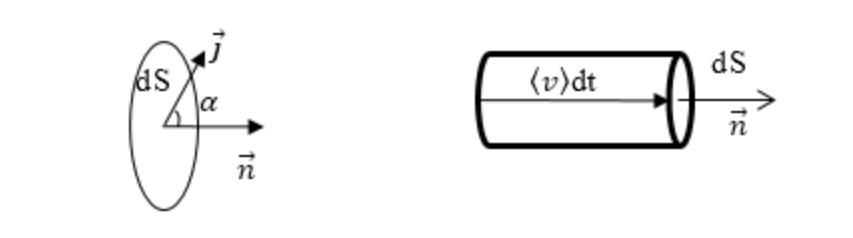
Рисунок
Проиллюстрируем на поверхности площадки очень короткий прямой цилиндр, имеющий высоту . Весь массив частиц, которые располагались внутри такого цилиндра за время пересекут плоскость и перенесут через нее, в направлении скорости , заряд, выражающийся в виде следующего выражения:
,
где является зарядом электрона, другими словами отдельной частицы или же носителя тока. Разделим приведенную формулу на и получим:
,
где представляет собой модуль плотности электрического тока.
,
где является модулем плотности электрического тока в проводнике, в котором заряд переносится электронами. В случае, если ток появляется как результат движения нескольких типов зарядов, то формула плотности тока может быть определена в виде следующего выражения:
,
где представляет собой носитель заряда. Плотность тока — это векторная величина. Снова обратим внимание на рисунок . Пускай представляет собой единичный перпендикуляр к плоскости . В случае, если частицы, переносящие заряд, являются положительными, то переносимый ими заряд в направлении нормали больше нуля. В общем случае переносимый в единицу времени элементарный заряд может быть записана в следующем виде:
.
Формула приведенная выше справедлива также в том случае, когда плоскость площадки неортогональная по отношению к вектору плотности тока. По той причине, что составляющая вектора , направленная под прямым углом к нормали, через сечение электричества не переносит. Исходя из всего вышесказанного, плотность тока в проводнике окончательно запишем, применяя формулу в таком виде:
.
Таким образом, плотность тока эквивалентна количеству электричества, другими словами заряду, который протекает за одну секунду через единицу сечения проводника. В отношении однородного цилиндрического проводника справедливым будет записать, что:
,
где играет роль площади сечения проводника. Плотность постоянного тока равна по всей площади сечения проводника. Для двух разных сечений проводника с постоянным током справедливо следующее равенство:
.
Основываясь на законе Ома для плотности токов можно записать такое выражение:
,
где обозначает коэффициент удельной электропроводности. Определив плотность тока, мы имеем возможность выразить силу тока в следующем виде:
,
где интегрирование происходит по всей поверхности любого сечения проводника. Единица плотности тока .
Линии тока
Линии, вдоль которых движутся заряженные частицы, носят название линий тока.
Направления движения положительных зарядов также определяются в качестве направлений линий тока. Изобразив линии тока, можно получить наглядное представление о движении электронов и ионов, которые формируют собой ток. Если внутри проводника выделить трубку с током, у которой боковая поверхность состоит из линий тока, то движущиеся заряженные частицы не будут пересекать боковую поверхность данной трубки. Такую трубка представляет собой так называемую трубку тока. К примеру, поверхность металлической проволоки в изоляторе будет определяться как труба тока.
Сила тока в проводнике равномерно возрастает от до на протяжении . Определите заряд, который прошел через поперечное сечение проводника за данный отрезок времени.
Решение
В качестве основы решения данной задачи возьмем формулу, которая характеризует собой силу тока, то есть:
.
Таким образом, заряд будет найден как:
.
В условии задачи сказано, что сила тока изменяется равномерно, а это означает то, что мы можем записать закон изменения силы тока в следующем виде:
.
Найдем коэффициент пропорциональности в приведенном выражении, для чего необходимо запишем закон изменения силы тока еще раз для момента времени, при котором сила тока эквивалентна :
.
Подставим выражение выше в и проинтегрируем в соответствии с , получим формулу такого вида: .
В качестве начального момента времени возьмем момент, когда сила тока эквивалентна нулю, другими словами . Проведем следующие вычисления:
.
Ответ: .
Определите среднюю скорость движения электронов в проводнике, молярная масса вещества которого эквивалентна , поперечное сечение проводника . Сила тока в проводнике . Примем, что на каждый атом вещества в проводнике приходится два свободных электрона.
Решение
Силу тока в проводнике можно считать постоянной, что позволяет нам записать следующее выражение:
,
где заряд определим как произведение числа электронов проводимости в проводнике, на заряд одного электрона , представляющего собой известную величину. играет роль промежутка времени, за который через поперечное сечение проводника проходит заряд . Найти можно, если применять известное в молекулярной физике соотношение:
,
где играет роль количества атомов в проводнике, объем которого , плотность , а молярная масса . представляет собой число Авогадро. По условию задачи . Найдем из число свободных электронов: .
Подставим выражение, приведенное выше, в , в результате чего получим:
,
где объем проводника найден как , где - длина проводника. Выразим ее.
.
Среднюю скорость движения электронов или, другими словами, скорость тока в проводнике можно определить следующим образом: .
Ответ: .
Навигация по статьям
