
Статью подготовили специалисты образовательного сервиса Zaochnik.
Вязкое трение и сопротивление среды
Содержание:
Отличие вязкого трения от сухого заключается в том, что оно способно обращаться в ноль одновременно со скоростью. Даже при малой внешней силе может быть сообщена относительная скорость слоям вязкой среды.
Сила сопротивления при движении в вязкой среде
Кроме сил трения при движении в жидких и газообразных средах возникают силы сопротивления среды, которые проявляются намного значительней, чем силы трения.
Поведение жидкости и газа по отношению к проявлениям сил трения не отличаются. Поэтому, приведенные ниже характеристики, относят к обоим состояниям.
Действие силы сопротивления, возникающей при движении тела в вязкой среде, обусловлено ее свойствами:
- отсутствие трения покоя, то есть передвижение плавающего многотонного корабля при помощи каната;
- зависимость силы сопротивления от формы движущегося тела, иначе говоря, от ее обтекаемости для уменьшения сил сопротивления;
- зависимость абсолютной величины силы сопротивления от скорости.
Сила вязкого трения
Существуют определенные закономерности, которым подчинены и силы трения и сопротивления среды с условным обозначением суммарной силы силой трения. Ее величина находится в зависимости от:
- формы и размеров тела;
- состояния его поверхности;
- скорости относительно среды и ее свойства, называемого вязкостью.
Для изображения зависимости силы трения от скорости тела по отношению к среде используют график рисунка .
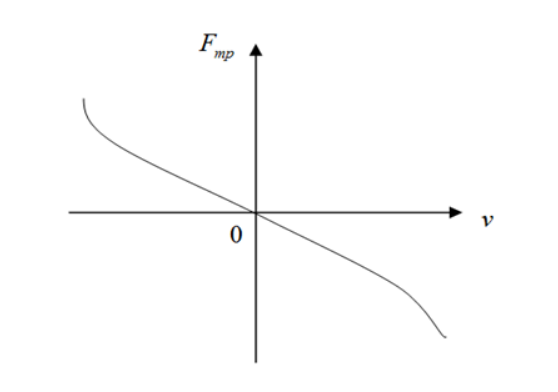
Рисунок . График зависимости силы трения от скорости по отношению к среде
Если значение скорости мало, то сила сопротивления прямо пропорциональна относительно , а сила трения линейно увеличивается со скоростью:
.
Наличие минуса означает направление силы трения в противоположную сторону относительно направления скорости.
При большом значении скорости происходит переход линейного закона в квадратичный, то есть рост силы трения пропорционально квадрату скорости:
.
Если в воздухе уменьшается зависимость силы сопротивления от квадрата скорости, говорят о скоростях со значениями нескольких метров в секунду.
Величина коэффициентов трения и находится в зависимости от формы, размера и состояния поверхности тела и вязких свойств среды.
Если рассматривать затяжной прыжок парашютиста, то его скорость не может постоянно увеличиваться, в определенный момент начнется ее спад, при котором сила сопротивления приравняется к силе тяжести.
Значение скорости, при котором закон производит переход в , зависит от тех же причин.
Происходит падение двух различных по массе металлических шариков с одной и той же высоты с отсутствующей начальной скоростью. Какой из шаров упадет быстрее?
Дано:
Решение
Во время падения оба тела набирают скорость. В определенный момент движение вниз производится с установившейся скоростью, при которой значение силы сопротивления приравнивается силе тяжести:
.
Получаем установившуюся скорость по формуле:
.
Следовательно, тяжелый шарик обладает большей установившейся скоростью падения, чем легкий. Поэтому достижение земной поверхности произойдет быстрее.
Ответ: тяжелый шарик быстрее достигнет земли.
Парашютист летит со скоростью до раскрытия парашюта, а после – со скоростью . Определить силу натяжения строп при раскрытии парашюта. Масса парашютиста , ускорение свободного падения . Обозначить пропорциональность относительно .
Дано: .
Найти: - ?
Решение
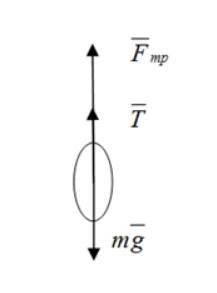
Рисунок
Перед раскрытием парашютист обладал скоростью , то есть его ускорение было равным нулю.
По второму закону Ньютона получаем:
.
Очевидно, что
.
После того, как парашют раскрылся, его меняется и становится равной . Отсюда второй закон Ньютона примет вид:
.
Для нахождения силы натяжения строп необходимо преобразовать формулу и подставить значения:
.
Ответ: .
Навигация по статьям
