Космические скорости

Содержание:

Преподаватель физики

Чтобы внести ясность в то, какие необходимы условия для того, чтобы тело стало искусственным спутником Земли, предложен рисунок $1$ . Это копия ньютоновского чертежа. Изображение земного шара дополнено высокой горой, с вершины которой производят бросание камней, придавая им различные по модулю и горизонтально направленные скорости. Действие силы тяжести способствует отклонению движущихся камней от прямолинейного пути. После описания кривой траектории он падает на Землю.

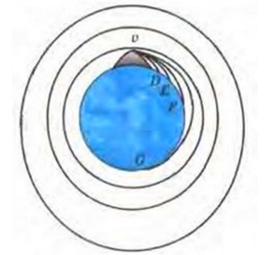
Рисунок $1$

Если прилагать больше сил при бросании, то он упадет дальше. Отсюда следует, что при отсутствии сопротивления воздуха и при наличии большой скорости тело может даже не приземляться на поверхность. Это говорит о его дальнейшем описывании круговых траекторий, не изменяя высоты относительно земной поверхности.

Первая космическая скорость

Чтобы движение вокруг Земли проходило по круговой орбите с радиусом, схожим с земным $R_{з}$ , тело должно обладать определенной скоростью $υ_{1}$ , которую можно определить из условия равенства произведения массы тела на ускорение силы тяжести, действующей на тело.

Определение 1

Для того, чтобы какое-либо тело могло стать спутником Земли, ему должна быть сообщена скорость $υ_{1}$ , называемая первой космической. При подстановке значений $g$ и $R_{з}$ в формулу, получаем, что

$υ_{1} = \sqrt{g R_{з}} = 8 к м / с$ .

Вторая космическая скорость

Определение 2

Если тело обладает скоростью $υ_{1}$ , то впоследствии при движении не упадет. Но значения
$υ_{1}$ недостаточно для выхода из сферы земного притяжения, то есть удалиться от Земли на расстояние, при котором оно теряет свою силу. Для этого нужна скорость $υ_{x}$ , которая получила название второй космической или скорость убегания.

Для ее нахождения следует произвести вычисление работы, потраченную против сил земного притяжения для соударения с поверхности Земли на бесконечность. При удалении такого тела получаем:

$\frac{m υ_{2}^{2}}{2} - G \frac{m M}{R} = 0, R = h + r$

где $m$ – масса брошенного тела, $М$ – масса планеты, $r$ – радиус планеты, $h$ – длина от основания до его центра масс, $G$ – гравитационная постоянная, $υ_{2}$ - вторая космическая скорость.

Решив уравнение относительно $υ_{2}$ , получим:

$υ_{2} = \sqrt{2 G \frac{M}{R}}$ .

Существует связь между первой и второй скоростями

$υ_{2} = \sqrt{2} υ_{1}$ .

Квадрат скорости убегания равняется ньютоновскому потенциалу в заданной точке, то есть:

$υ_{2}^{2} = - 2 Φ = 2 \frac{G M}{R}$ .

Скорость $υ_{2}$ считается за вторую космическую. Из сравнений видно, что она в $\sqrt{2}$ раза больше первой. Если умножить $8 к м / с$ на $\sqrt{2}$ , то получим значение для $υ_{2}$ , приблизительно равняющееся $11 к м / с$ .

Замечание 1

Нужная величина скорости не зависит от направления движения тела. На это влияет вид траектории, по которой происходит удаление от земной поверхности.

Чтобы тело смогло стартовать с поверхности планеты, оно должно обладать второй космической скоростью при малом значении $h$ и большом значении гравитационной силы. Как только ракета начнет удаляться от Земли, гравитационная постоянная будет уменьшаться вместе со значением, необходимым для убегания кинетической энергии.

Третья космическая скорость

Определение 3

Для выхода за пределы Солнечной системы телу следует преодолеть как силу притяжения к Земле, так и к Солнцу. Для этого применяется третья космическая скорость $υ_{3}$ , позволяющая запускать тело с земной поверхности.

Значение $υ_{3}$ зависит от направления. Если запуск производится в направлении орбитального движения Земли, тогда ее значение минимально и составит около $17 к м / с$ . Когда тело запущено противоположно направлению движения Земли, тогда значение скорости $υ_{3} \approx 73$ .

Замечание 2

Еще в СССР были достигнуты космические скорости.

Первый запуск искусственного спутника был осуществлен $4$ октября $1957$ года.
Уже $2$ января $1959$ ученым удалось найти решения для преодоления сферы земного притяжения. Поэтому запущенная ракета стала первой космической планетой Солнечной системы.
Дата $12$ апреля $1961$ года известна, так как был осуществлен полет человека в космическое пространство. Юрий Алексеевич Гагарин был первым советским космонавтом, совершившим один оборот вокруг Земли, после чего благополучно приземлился.

Пример 1

Определить первую космическую скорость для спутника Юпитера, летающего на небольшой высоте, если дана масса планеты, равная $1, 9 \cdot 10^{27} к г$ , а ее радиус $R = 7, 13 \cdot 10^{7} м$ .

Дано:

$B = 1, 9 \cdot 10^{27} к г$ ,

$R = 7, 13 \cdot 10^{7} м$ .

Найти: $υ_{1}$ - ?

Решение

Для начала запишем формулу для нахождения первой космической скорости: $υ_{1} = \sqrt{g R_{3}} (1)$ .

Значение $g$ принимает ускорение свободного падения на Юпитере.

Из закона всемирного тяготения получаем, что $m g = G \frac{M m}{r^{2}} (2)$ .

Значение $m$ определено как масса спутника, а $М$ – масса самой планеты.

Если высота спутника над поверхностью Юпитера сравнительно мала относительно его радиуса, тогда ею разрешено пренебречь: $r = R$ .

Получаем, что из уравнения $(2)$ найдем ускорение свободного падения для планеты из

$g = G \frac{M}{R^{2}}$ .

После подстановки в уравнение $(1)$ , сможем найти первую космическую скорость.

$υ_{1} = \sqrt{G \frac{M}{R}} = 42159, 45 м / с$ .

Ответ: $υ_{1} = 42159, 45 м / с$ .

Курсовая работа по физике

от 5 дней/ от 2160 р.

Реферат по физике

от 1 дня/ от 840 р.

Решение задач по физике

от 1 дня/ от 150 р.