
Статью подготовили специалисты образовательного сервиса Zaochnik.
Движение центра масс системы
Содержание:
Допустим, что у нас есть некоторая система, состоящая из -ного количества материальных точек. Возьмем одну из них и обозначим ее массу как . Приложенные к точке внешние силы (как активные силы, так и реакции связей) имеют равнодействующую . Внутренние силы имеют равнодействующую . Наша система находится в движении, следовательно, нужная точка будет иметь ускорение . Зная основной закон динамики, мы можем записать следующую формулу:
.
Ее можно применить к любой точке системы. Значит, для всей системы целиком можно сформулировать следующие уравнения:
Данная формула состоит из дифференциальных уравнений, описывающих движение системы в векторной форме. Если мы спроецируем эти равенства на соответствующие координатные оси, то у нас получатся дифференциальные уравнения движения в проекциях. Но в конкретных задачах чаще всего вычислять движение каждой точки системы не требуется: можно ограничиться характеристиками движения всей системы в целом.
Движение центра масс: основная теорема
Характер движения системы можно определить, зная закон, по которому движется ее центр масс.
Центр инерции системы (центр масс) – это воображаемая точка с радиус-вектором , выражаемым через радиус-векторы соответствующих материальных точек по формуле .
Здесь сумма показателей в числителе выражает общую массу всей системы.
Для нахождения этого закона нам нужно взять уравнения движения системы, приведенные в предыдущем пункте, и сложить их правые и левые части. У нас получится, что:
.
Взяв формулу радиус-вектора центра масс, получим следующее:
.
Теперь возьмем вторую производную по времени:
.
Здесь буквой обозначено ускорение, которое приобретает центр масс системы.
Свойство внутренних сил в системе гласит, что равно нулю, значит, окончательное равенство будет выглядеть так:
.
Это уравнение является записью закона движения центра масс. Запишем его:
Движение центра масс системы идентично движению материальной точки той же массы, что и вся система целиком, к которой приложены все действующие на систему внешние силы.
Иначе говоря, произведение ускорения центра масс системы на массу самой системы будет равно геометрической сумме всех внешних сил, действующих на эту систему.
Возьмем полученное выше уравнение и спроецируем его правую и левую части на соответствующие координатные оси. У нас получится:
.
Эти равенства являются дифференциальными уравнениями движения центра масс в проекции на оси в декартовой системе координат.
Практическое значение теоремы о движении центра масс
Данная теорема имеет большую практическую ценность. Поясним, в чем именно она заключается.
- Любое тело, движущееся поступательно, может быть рассмотрено в качестве материальной точки, масса которой равна массе всего тела. Во всех других случаях такой подход возможен лишь тогда, когда для определения положения тела в пространстве нам будет достаточно знать, в каком положении находится его центр масс. Также важно, чтобы условия задачи допускали исключение вращательной части движения тела.
- С помощью теоремы движения центра масс системы мы можем не рассматривать в задачах неизвестные нам заранее внутренние силы.
Разберем пример применения теоремы для решения практической задачи.
Условие: к оси центробежной машины на нити подвешено кольцо из металла. Оно совершает равномерные вращательные движения с угловой скоростью, равной . Вычислите, на каком расстоянии центр кольца находится от оси вращения.
Решение
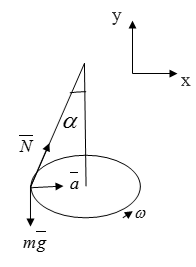
Очевидно, что система находится под воздействием силы тяжести . Также необходимо учесть силу натяжения нити и центростремительное ускорение.
Второй закон Ньютона для системы будет выглядеть так:
.
Теперь создадим проекции обеих частей равенства на оси абсцисс и ординат и получим:
Мы можем разделить одно уравнение на другое:
.
Поскольку , то нужное нам уравнение будет выглядеть так:
.
Ответ: .
Навигация по статьям
