
Статью подготовили специалисты образовательного сервиса Zaochnik.
Закон распределения молекул по скоростям
Содержание:
С помощью закона распределения молекул по скоростям мы можем описать, как именно в макроскопической системе происходит распределение частиц (при условии ее нахождения в термодинамическом равновесии). Такое распределение называется стационарным, и воздействия внешних сил на систему при этом не происходит.
Данный закон распространяется как на жидкости, так и на газы, если на них действуют законы классической механики. Если мы знаем, как именно распределяются молекулы по своим скоростям, значит, мы можем ответить, какой объем молекул имеет определенную скорость в условиях заданной температуры в равновесном состоянии.
Чтобы лучше объяснить данный вопрос, начнем с введения такого понятия, как пространство скоростей. Оно изображено схематически на рисунке .
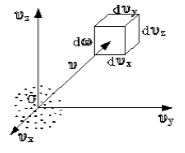
Рисунок
Мы видим, что в декартовой системе координат здесь отмечены именно проекции скоростей, а не координаты. Тогда исходный вопрос можно переформулировать так: "Как именно будут распределяться молекулы в пространстве скоростей"?
Очевидно, что данное распределение не будет равномерным. Если в пространстве мы выделим параллелепипед, имеющий объем , то в нем окажется молекул. Обозначим буквой число молекул газа, тогда будет некоторой функцией скорости.
Распределение Максвелла
Поскольку, как мы уже отмечали, газ находится в равновесном состоянии, то направления движений частиц являются равноправными. Значит, допустимо считать, что в пространстве скоростей распределение молекул является симметричным и имеет сферическую форму.
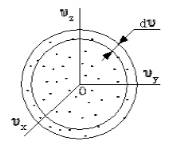
Рисунок
Определим, из скольких молекул состоит шаровой слой . Разделим найденное выше число на количество частиц и получим вероятность того, что пределы модуля скорости молекулы равны .
Здесь является функцией распределения вероятности значения . Впервые данная функция теоретически была получена Д. Максвеллом.
Таким образом, закон распределения молекул по модулям скоростей имеет следующий вид:
.
Здесь , масса молекулы равна , а – постоянная Больцмана.
По проекциям скоростей распределение Максвелла может быть записано так:
.
Важно учесть, что:
.
Параметры означают проекции скоростей молекул на оси координат.
Также возможен следующий вариант записи распределения Максвелла:
.
Здесь обозначает наиболее вероятную скорость движения молекулы.
Как выглядит распределение Максвелла на графике
Кривая распределения молекул по скоростям на графике выглядит так:
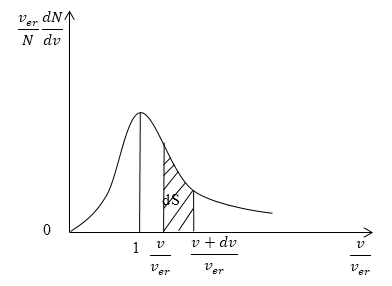
Рисунок
При этом доля тех молекул, которые движутся со скоростями в интервале от до будет пропорциональна площади , которая на графике обозначена штриховкой.
Скорости всех молекул принадлежат интервалу от нуля до плюс бесконечности, значит, будет верным равенство:
.
Оно называется условием нормировки функции распределения.
Следовательно, распределение Максвелла по скоростям имеет зависимость от температуры газа и массы его молекул. Объем и давление можно не учитывать.
Условие: вычислите, какова будет наиболее вероятная скорость молекул газа при температуре в равновесном состоянии.
Решение
Нам потребуется распределение Максвелла (распределение по модулям скоростей).
.
Максимум функции будет соответствовать самой вероятной скорости. Дифференциация выражения по скорости и сравнение ее с нулем даст нам следующий результат:
;
.
.
Ответ: наиболее вероятно, что скорость газа будет равна .
Условие: изобразите кривые распределения скоростей молекул газа при росте температуры .
Решение
Возьмем формулу наиболее вероятной скорости из предыдущей задачи.
Понятно, что чем больше будет температура, тем выше будет скорость молекул, т.е. произойдет смещение максимума в сторону больших скоростей. Поскольку площадь под кривой распределения является постоянной величиной, кривые на графике будут показаны следующим образом:
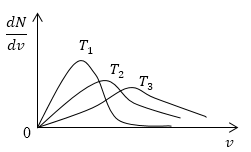
Рисунок
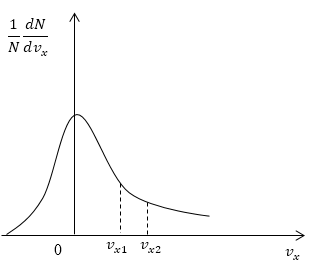
Условие: дан график функции, по которой молекулы будут распределяться с учетом проекций скорости . Сопоставьте количества молекул, проекции скорости которых будут принадлежать интервалам от нуля до и от до .
Рисунок
Решение
Как мы уже указывали ранее, доля молекул газа, скорости которых лежат в первом интервале, будет пропорциональна площади фигуры, образуемой кривой распределения, вертикальной осью и вертикальным пунктиром, перпендикулярным оси проекций. Во втором интервале нужная доля будет пропорциональна площади фигуры, ограниченной кривой распределения и вертикальной прямой, параллельной оси и проходящей через точку . Очевидно, что площадь первой фигуры будет меньше площади второй. Значит, и молекул, проекции скоростей которых лежат в первом интервале, будет меньше, чем во втором.
Ответ: молекул, имеющих проекции скорости в интервалах: от до меньше, чем молекул, имеющих проекции скорости в интервалах: от до .
Навигация по статьям
