
Статью подготовили специалисты образовательного сервиса Zaochnik.
Средняя скорость молекул
Содержание:
В физике выделяют скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.
Средняя скорость движения молекул
Средняя скорость движения молекул называется также скоростью теплового движения молекул.
Формула средней относительной скорости молекул в физике представлена следующим выражением:
.
Средняя квадратичная скорость
Средняя квадратичная скорость движения молекул газа это следующая величина:
Формулу средней квадратичной скорости можно переписать так:
.
Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:
Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:
,
где – это концентрация частиц вещества, – это количество частиц вещества, – это объем.
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок ).
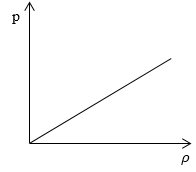
Рисунок
Решение
Запишем выражение для средней скорости движения молекул газа следующим образом:
Из графика видно, что или , где – это некоторая константа.
Подставив в , получаем:
Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.
Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа , молярная масса газа , а также концентрация молекул газа ?
Решение
Применим выражение для :
Помимо этого, из уравнения Менделеева-Клайперона и зная, что :
.
Поделим правую и левую части на , и зная , получаем:
Подставляем в выражение для среднеквадратичной скорости , получаем:
Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы .
Навигация по статьям
