
Статью подготовили специалисты образовательного сервиса Zaochnik.
Скорость и ускорение в сферических координатах
Содержание:
Движение в пространстве может быть задано, если известен закон изменения трех декартовых координат в качестве функции времени.
Имеются случаи, когда перемещение материальной точки не может быть описано с помощью уравнения движения в декартовых координатах, так как запись становится громоздкой. Тогда следует выбирать три независимые скалярные параметра , называемые криволинейными (обобщенными) координатами, которые способны четко определить положение точки в пространстве.
Вектор скорости
Определение точки во время задания ее движения в криволинейных координатах возможно в виде векторной суммы составляющих скоростей, параллельных координатным осям:
.
Запись проекции вектора скорости на соответствующие координаты оси примет вид:
.
является параметром, называющимся - м коэффициентом Ламе и равняющимся значению модуля частной производной от радиус-вектора точки по - ой криволинейной координате, которая была вычислена в данной точке .
Направление каждого из векторов соответствует направлению движения точки конца радиус-вектора при возрастании - й обобщенной координаты.
Расчет модуля скорости в ортогональной криволинейной системе координат рассчитывается по формуле:
.
Чтобы вычислить текущее положение точки , необходимо найти производные и коэффициенты Ламе приведенных формул в пространстве.
В сферической системе координат координатами точки являются скалярные параметры , отсчитываемые так, как изображено на рисунке .
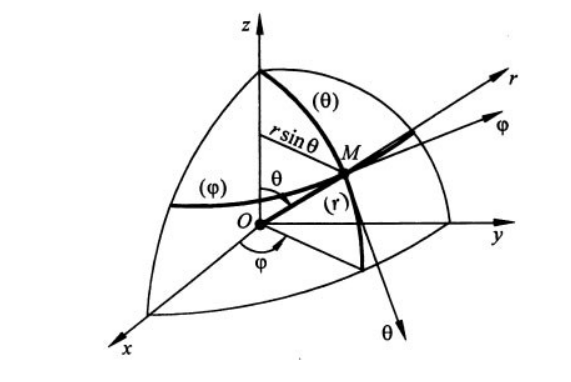
Рисунок . Вектор скорости в сферической системе координат
Ускорение системы
Составленная система уравнений движения точки запишется как:
.
На рисунке показаны радиус-вектор, проведенный из начала координат, углы и , координатные линии, оси рассматриваемой системы в произвольной точке траектории.
Расположение координатных линий и идет на поверхности сферы радиусом . Данная система получила название ортогональной.
Выражение декартовых координат возможно через сферические:
.
Отсюда следует, что коэффициенты Ламе , проекции скорости точки на оси сферической системы координат , а модуль вектора скорости .
Запись ускорения в сферических координатах примет вид:
.
А проекции ускорения точки:
Изображение модуля ускорения будет равняться .
Задана точка, которая производит движение по линии пересечения сферы и цилиндра по уравнению , где являются сферическими координатами.
Произвести поиск модуля и проекции скорости точки на оси сферической системы координат.
Решение
Необходимо найти проекции вектора скорости на оси сферических координат.
Получим:
.
Определяем модуль скорости:
.
Применив условие предыдущего задания, определить модуль ускорения точки.
Решение
Произведем нахождение проекции вектора ускорения на оси сферических координат.
Получаем, что:
Далее определим модуль ускорения: .
Ответ:
Навигация по статьям
