
Статью подготовили специалисты образовательного сервиса Zaochnik.
Равноускоренное движение: формулы, примеры
Содержание:
Равноускоренное движение
Равноускоренное движение - это движение, при котором вектор ускорения не меняется по модулю и направлению (в случае равнозамедленного движения модуль скорости равномерно меняется). Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение, в отличие от неравномерного, - частный случай ускоренного в равной степени движения с ускорением, равным нулю.
Рассмотрим случай свободного падения (тело брошено под углом к горизонту) более подробно с вычислением. Такое движение можно рассчитать и представить в виде суммы движений относительно вертикальной и горизонтальной осей.
Как найти ускорение в физике? Нахождение ускорения в физике происходит с учетом того, что в любой точке траектории на тело действует ускорение свободного падения , которое не меняется по величине и всегда направлено в одну сторону.
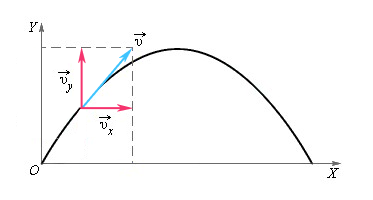
Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y - движение равноускоренное и прямолинейное. Будем рассматривать определенные проекции векторов скорости и ускорения на оси.
Формулы для равноускоренного движения
Формула для скорости (формула ускорения) при равноускоренном движении:
.
Здесь - начальная скорость тела, - ускорение.
Покажем на графике, что при равноускоренном движении зависимость имеет вид прямой линии. Вот небольшой тест.
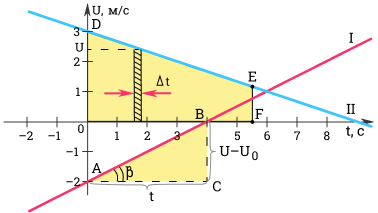
Как найти ускорение? Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC. Вот как выглядит формула ускорения в физике.
Чем больше угол , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.
Для первого графика: .
Для второго графика: .
По данному графику физик может также вычислить (произвести определение) перемещение тела за время . Как это сделать?
Выделим на графике малый отрезок времени . Будем считать, что он настолько мал, что движение за время можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка . Тогда, перемещение за время будет равно .
Разобьем все время на бесконечно малые промежутки . Перемещение за время равно площади трапеции .
.
Мы знаем, что , поэтому окончательная формула или расчет для перемещения тела примет вид:
Для того чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение (расстояние). Изменение координаты в зависимости от времени выражает закон равноускоренного движения.
Какова будет формула пути при равноускоренном движении? В этом случае путь изменяется согласно квадратной зависимости: 8=v0t + at²/2.
Закон равноускоренного движения
.
Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения - находить координаты при заданных значениях начальной и конечной скоростей и ускорения.
Исключая из записанных выше уравнений и решая их, получаем:
.
По известным начальной скорости, ускорению и перемещению может находиться конечная скорость тела:
.
При и
Величины , входящие в выражения, являются алгебраическими величинами. Они могут принимать как положительные, так и отрицательные значения - это будет зависеть от характера движения и направления координатных осей в условиях конкретной задачи.
Навигация по статьям
