Равномерное движение

Равномерное движение

Равномерное движение - движение вдоль прямой линии с постоянной (как по модулю, так и по направлению) скоростью. При равномерном движении пути, которые тело проходит за равные промежутки времени, также равны.

Для кинематического описания движения расположим ось OХ вдоль направления движения. Для определения перемещения тела при равномерном прямолинейном движении достаточно одной координаты Х. Проекции перемещения и скорости на координатную ось можно рассматривать, как алгебраические величины. 

Пусть в момент времени $t_1$ тело находилось в точке с координатой $x_1$, а в момент времени  $t_2$ - в точке с координатой $x_2$. Тогда проекция перемещения точки на ось OХ будет запишется в виде:

$∆s=x_2-x_1$.

В зависимости от направления оси и направления движения тела эта величина может быть как положительной, так и отрицательной. При прямолинейном и равномерном движении модуль перемещения тела совпадает с пройденным путем. Скорость равномерного прямолинейного движения определяется по формуле:

$v=\frac{∆s}{∆t}=\frac{x_2-x_1}{t_2-t_1}$

Если $v>0$, тело движется вдоль оси OX в положительном направлении. Иначе - в отрицательном. 

Математическое описание равномерного прямолинейного движения

Закон движения тела при равномерном прямолинейном движении описывается линейным алгебраическим уравнением.

Пример графика равномерного движения - на рисунке ниже.

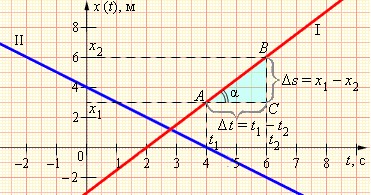
Здесь два графика, описывающих движение тел 1 и 2. Как видим, тело 1 во время $t=0$ находилось в точке $x=-3$.

От точки $x_1$ до точки $x_2$ тело переместилось за две секунды. Перемещение тела составило три метра.

$∆t=t_2-t_1=6-4=2с$

$∆s=6-3=3м$.

Зная это, можно найти скорость тела. 

$v=\frac{∆s}{∆t}=1,5\raisebox{1ex}{$м$}\!\left/ \!\raisebox{-1ex}{${с}^2$}\right.$

Есть еще один способ определения скорости: из графика ее можно найти как отношение сторон BC и AC треугольника ABC. 

$v=\frac{∆s}{∆t}=\frac{\left|BC\right|}{\left|AC\right|}$.

Причем, чем больше угол, который образует график с осью времени, тем больше скорость. Говорят также, что скорость равна тангенсу угла $\alpha$.

Аналогично вычисления проводятся для второго случая движения. Рассмотрим теперь новый график, изображающий движение с помощью отрезков прямых. Это так называемый кусочно-линейный график.

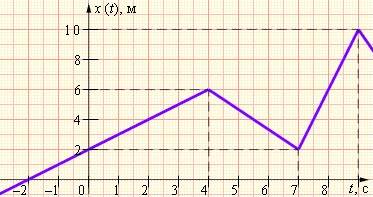
Движение, изображенное на нем - неравномерное. Скорость тела меняется мгновенно в точках излома графика, а каждый отрезок пути до новой точки излома тело движется равномерно с новой скоростью.

Из графика мы видим, что скорость менялась в моменты времени $t=4c, t=7с, t=9с$. Значения скоростей  также легко находятся из графика.

Отметим, что путь и перемещение не совпадают для движения, описываемого кусочно-линейным графиком. Например, в интервале времени от нуля до семи секунд тело прошло путь, равный 8 метрам. Перемещение тела при этом равно нулю.