
Статью подготовили специалисты образовательного сервиса Zaochnik.
Принципиальные методы измерения напряженности
Содержание:
Способом измерить напряженность электрического поля является принципиальный способ измерения векторов
Обычный метод измерения напряженности
Стоит заметить, что за обычный принимают метод измерения напряженности поля по силе, воздействующей на пробный заряд, который помещен в поле. Но такой способ возможно применять и для поля в вакууме, при этом метод не всегда подходит для поля в веществе. Так как равенство:
верно для вакуума, в веществе оно является приближенным. Сам процесс внесения пробного заряда в диэлектрик может оказаться невозможен, например, когда используемый диэлектрик - твердый.
Единственный способ измерения
Отметим при этом, что поле, измеренное подобным образом, не совпадет ни с вектором напряженности, ни с вектором индукции электрического поля. Итоговый результат будет зависеть от формы полости, в связи с чем в целях применения принципиального метода используют специальные формы полостей, в которых результат измерений
Измерение векторов поля при помощи полостей
Возьмем для рассмотрения полость, имеющую форму длинного и тонкого цилиндрического канала. Этот канал является параллельным полю
В конечном счете мы приходим к тому, что измерение поля в диэлектрике есть измерение поля
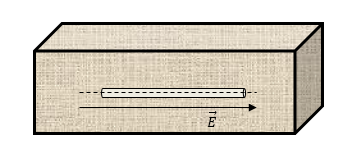
Рисунок
Рассмотрим другую форму плоскости: пусть это будет бесконечно короткий цилиндр, у которого основания являются перпендикулярными вектору индукции электрического поля
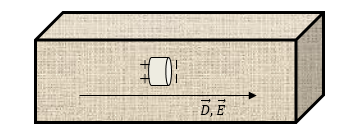
Рисунок
Удалив в этом случае из диэлектрика вещество, мы не получим существенного влияния на электрическое поле в диэлектрике в целом. На границах полости появятся поляризационные заряды, имеющие противоположные знаки. За пределами полости будет происходить почти полная компенсация полей зарядов друг другом. В пределах полости поля зарядов будут усиливать друг друга, что повлечет за собой значимое изменение поля внутри полости. В пределах полости
перпендикулярно к ее основаниям (в силу симметрии). Так как полость содержит воздух или вакуум:
Применим граничное условие и можем сделать следующий вывод:
Измерение электрического смещения сводится к измерению напряженности поля в полости.
Пусть задан шар, имеющий равномерную заряженность (объемная плотность ). Пусть в заданном шаре создана небольшая сферическая полость с центром . Центр созданной полости расположен на расстоянии от центра заданного диэлектрического шара . Необходимо определить напряженность поля в центре полости.
Решение
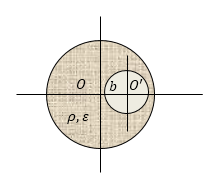
Рисунок
Чтобы найти поле в полости, применим теорему Остроградского - Гаусса совместно с принципом суперпозиции. Определять поле будем в точке , для чего создадим гипотетическую сферу, имеющую радиус и центр в точке . Запишем выражение для нахождения потока вектора электрического смещения сквозь поверхность данной сферы:
, где . Для поля шара присуща сферическая симметрия, тогда из выражения запишем:
.
Поляризационные заряды в полости создадут поле ; согласно принципу суперпозиции итоговое поле в точке определяется как:
.
Полость не имеет свободных зарядов, тогда, согласно теореме Остроградского-Гаусса:
.
Граничные условия определяют тот факт, что нормальная составляющая вектора электрического смещения при переходе через границу раздела диэлектриков неизменна. Таким образом:
.
Резюмируя все наши рассуждения, сделаем запись выражения для поля внутри полости:
.
Напряженность поля в полости определится как:
.
Ответ: поле в полости , где
Задана бесконечно длинная цилиндрическая полость, расположенная в бесконечно длинном цилиндре, который равномерно заряжен по объему ( – плотность заряда) и имеет радиус . Оси цилиндра и полости параллельны и удалены на некоторое расстояние друг от друга. Необходимо определить напряженность электрического поля на оси полости.
Решение
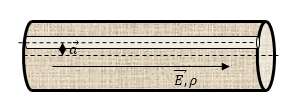
Рисунок 4
Чтобы определить поле в полости, применим теорему Остроградского – Гаусса совместно с принципом суперпозиции. Чтобы найти поле цилиндра на прямой, где должна находиться ось полости, создадим гипотетическую цилиндрическую поверхность радиуса с осью, совпадающей с осью основного цилиндра. Запишем выражение для потока вектора электрического смещения сквозь поверхность заданного цилиндра:
, где ( является высотой цилиндра).
Для поля шара присуща цилиндрическая симметрия, тогда из выражения запишем:
.
Поляризационные заряды в полости создадут поле ; согласно принципу суперпозиции итоговое поле на оси полости определяется как:
.
Полость не имеет свободных зарядов, тогда, согласно теореме Остроградского-Гаусса:
.
Граничные условия определяют тот факт, что нормальная составляющая вектора электрического смещения при переходе через границу раздела диэлектриков неизменна. Таким образом:
.
Резюмируя все наши рассуждения, сделаем запись выражения для поля внутри полости:
.
Напряженность поля в полости определится как:
.
Ответ: .
Навигация по статьям
