
Статью подготовили специалисты образовательного сервиса Zaochnik.
Принцип суперпозиции электрических полей
Содержание:
Одна из задач, которые ставит электростатика перед собой – это оценка параметров поля при заданном стационарном распределении зарядов в пространстве. И принцип суперпозиции является одним из вариантов решения такой задачи.
Принцип суперпозиции
Предположим наличие трех точечных зарядов, находящихся во взаимодействии друг с другом. При помощи эксперимента возможно осуществить измерение сил, действующих на каждый из зарядов. Для нахождения суммарной силы, с которой на один заряд действуют два других заряда, нужно силы воздействия каждого из этих двух сложить по правилу параллелограмма. При этом логичен вопрос: равны ли друг другу измеряемая сила, которая действует на каждый из зарядов, и совокупность сил со стороны двух иных зарядов, если силы рассчитаны по закону Кулона. Результаты исследований демонстрируют положительный ответ на этот вопрос: действительно, измеряемая сила равна сумме вычисляемых сил согласно закону Кулона со стороны других зарядов. Данное заключение записывается в виде совокупности утверждений и носит название принципа суперпозиции.
Принцип суперпозиции:
- сила взаимодействия двух точечных зарядов не изменяется, если присутствуют другие заряды;
- сила, действующая на точечный заряд со стороны двух других точечных зарядов, равна сумме сил, действующих на него со стороны каждого из точечных зарядов при отсутствии другого.
Принцип суперпозиции полей заряда является одним из фундаментов изучения такого явления, как электричество: значимость его сопоставима с важностью закона Кулона.
В случае, когда речь идет о множестве зарядов (т.е. нескольких источников поля), суммарную силу, которую испытывает на себе пробный заряд , можно определить по формуле:
,
где является силой, с которой влияет на заряд заряд , если прочий заряд отсутствует.
При помощи принципа суперпозиции с использованием закона взаимодействия между точечными зарядами существует возможность определить силу взаимодействия между зарядами, присутствующими на теле конечных размеров. С этой целью каждый заряд разбивается на малые заряды (будем считать их точечными), которые затем берутся попарно; вычисляется сила взаимодействия и в заключение осуществляется векторное сложение полученных сил.
Полевая трактовка принципа суперпозиции
Полевая трактовка: напряженность поля двух точечных зарядов есть сумма напряженностей, создаваемым каждым из зарядов при отсутствии другого.
Для общих случаев принцип суперпозиции относительно напряженностей имеет следующую запись:
,
где является напряженностью -го точечного заряда, - радиусом вектора, проложенного от -го заряда в некоторую точку пространства. Указанная формула говорит нам о том, что напряженность поля любого числа точечных зарядов есть сумма напряженностей полей каждого из точечных зарядов, если другие отсутствуют.
Инженерная практика подтверждает соблюдение принципа суперпозиции даже для очень больших напряженностей полей.
Значимым размером напряженности обладают поля в атомах и ядрах (порядка ), но и в этом случае применялся принцип суперпозиции для расчетов энергетических уровней. При этом наблюдалось совпадение результатов расчетов с данными экспериментов с большой точностью.
Все же следует также заметить, что в случае очень малых расстояний (порядка ) и экстремально сильных полей принцип суперпозиции, вероятно, не выполняется.
Например, на поверхности тяжелых ядер при напряженности порядка принцип суперпозиции выполняется, а при напряженности возникают квантово-механические нелинейности взаимодействия.
Когда распределение заряда является непрерывным (т.е. отсутствует необходимость учета дискретности), совокупная напряженность поля задается формулой:
.
В этой записи интегрирование проводится по области распределения зарядов:
- при распределении зарядов по линии ( - линейная плотность распределения заряда) интегрирование проводится по линии;
- при распределении зарядов по поверхности ( - поверхностная плотность распределения) интегрирование проводится по поверхности;
- при объемном распределении заряда ( - объемная плотность распределения) интегрирование проводится по объему.
Принцип суперпозиции дает возможность находить для любой точки пространства при известном типе пространственного распределения заряда.
Примеры применения принципа суперпозиции
Заданы одинаковые точечные заряды , расположенные в вершинах квадрата со стороной . Необходимо определить, какая сила воздействует на каждый заряд со стороны других трех зарядов.
Решение
На рисунке проиллюстрируем силы, влияющие на любой из заданных зарядов в вершинах квадрата. Поскольку условием задано, что заряды одинаковы, для иллюстрации возможно выбрать любой из них. Сделаем запись суммирующей силы, влияющей на заряд :
.
Силы и являются равными по модулю, определим их так:
.
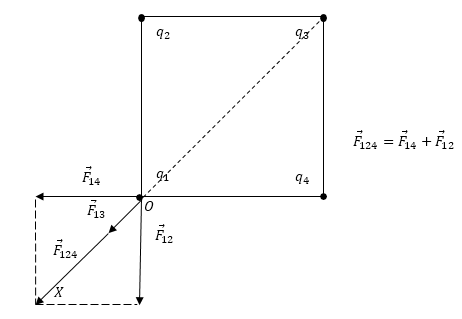
Рисунок
Теперь зададим направление оси (рисунок ), спроектируем уравнение , подставим в него полученные выше модули сил и тогда:
.
Ответ: сила, оказывающее воздействие на каждый из заданных зарядов, находящихся в вершинах квадрата, равна .
Задан электрический заряд, распределенный равномерно вдоль тонкой нити (с линейной плотностью ). Необходимо записать выражение, определяющее напряженность поля на расстоянии от конца нити вдоль ее продолжения. Длина нити – .
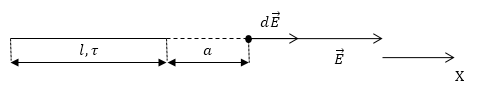
Рисунок
Решение
Первым нашим шагом будет выделение на нити точечного заряда . Составим для него, в соответствии с законом Кулона, запись, выражающую напряженность электростатического поля:
.
В заданной точке все векторы напряженности имеют одинаковую направленность вдоль оси ОХ, тогда:
.
Условием задачи дано, что заряд имеет равномерное распределение вдоль нити с заданной плотностью, и запишем следующее:
.
Подставим эту запись в записанное ранее выражение напряженности электростатического поля, проинтегрируем и получим:
.
Ответ: напряженность поля в указанной точке будет определяться по формуле .
Навигация по статьям
