
Статью подготовили специалисты образовательного сервиса Zaochnik.
Потенциальность электростатического поля
Содержание:
Потенциальное (консервативное) поле − это поле, в котором работа при перемещении зависит только лишь от конечной и начальной точки пути и не зависит от траектории движения тела.
Что такое потенциальное поле
Есть и другое абсолютно равнозначное определение потенциальности поля (консервативной силы).
Поле называется потенциальным, если при перемещении по любому замкнутому контуру работа сил поля равняется .
Известно, что сила гравитации , которая убывает обратно пропорционально квадрату расстояния, является потенциальной, при этом ее потенциальность обусловлена именно обратно пропорциональной зависимостью от расстояния. Сила Кулона тоже обратно пропорциональна квадрату расстояния. Напомним закон Кулона . Все математическое описание потенциала создавалось при изучении сил гравитации. Понятие о потенциале появилось в работах Ж. Л. Лагранжа в году. Определение «потенциал» было введено в науку намного позже Дж. Грином и К. Ф. Гауссом.
На основе принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.
Легко докажем это математически. Циркуляция вектора напряженности поля точечного заряда по любому замкнутому контуру равняется :
.
Если поле создает точечных зарядов, тогда по принципу суперпозиции результирующее поле находим как:
.
Находим интеграл:
.
Приведенный выше критерий потенциальности поля не дифференциален, поэтому его трудно применять. Нужно проверять равенство работы по замкнутому контуру. А это означает, что необходимо анализировать бесконечное число циклов, что, в конечном итоге, невозможно. Критерий потенциальности применим лишь в случае, когда известна аналитическая формула работы, что не всегда возможно. Поэтому нужно отыскать другой критерий потенциальности поля, который был бы прост в применении. Данным критерием является дифференциальная формулировка. Она определяется при помощи понятия ротор вектора .
Что такое ротор. Практические задачи
Ротор − это вектор, проекция которого на направление единичного вектора определяется таким образом:
,
где − это площадь, которая лежит в плоскости перпендикулярной к , ограниченная малым контуром , на контуре − это направление положительного обхода связано с правилом правого винта.
Обращаем внимание, что в формуле большой буквой обозначена площадь, а маленькой буквой − линейное перемещение.
Ротор описывает интенсивность «завихрения» вектора. На практике при вычислении ротора применяют следующие формулы:
.
Независимость работы от пути перемещения заряда в электростатическом поле выражается формулой:
.
где и − это различные пути между точками и . При замене местами пределов интегрирования получаем:
.
Выражение представим в виде:
.
где . Применяем формулу Стокса:
,
к уравнению выше, получаем:
,
где − это поверхность, ограниченная контуром . Поскольку поверхность произвольная, то интеграл в выражении может равняться , только если равняется подынтегральное выражение, а поскольку то есть:
.
Это дифференциальная формулировка потенциальности электростатического поля.
Необходимо найти для точек оси вращения, если − это вектор скорости точек твердого тела, вращающегося с угловой скоростью вокруг оси коллинеарной
Решение
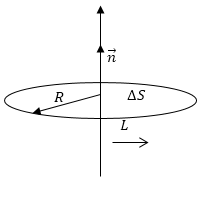
Рисунок
В качестве контура L выберем окружность радиусом R с центром на оси вращения, перпендикулярную оси (рисунок ). Известно, что:
Обозначим как скалярное значение элемента окружности. Для этого используем формулу определения ротора, получаем:
,
где − это длина окружности.
Ответ: Ротор линейной скорости точек вращающегося тела равняется .
Необходимо доказать, что из условия потенциальности поля следует: тангенциальные составляющие напряженности электростатического поля непрерывны.
Решение
Поскольку электростатическое поле потенциально, тогда выполняется равенство:
.
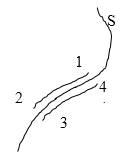
Рисунок
Тангенциальные составляющие − это касательные к произвольной поверхности в любой ее точке. Непрерывность значит, что значения касательных составляющих напряженности одинаковы по обеим сторонам поверхности.
Допустим обратное. Пускай вдоль поверхности (рисунок ) непрерывности нет. Это означает, что если и разделенные поверхностью , но бесконечно близкие друг к другу точки, тогда работа электростатических сил на пути отличается на конечную величину от работы тех же сил на пути . Так как мы считаем, что отрезки и бесконечно малы, силы конечны, значит, и работа, которую выполняют электрические силы на заданных отрезках, бесконечно малая величина. Выходит, что работа на пути не должна равняться . То есть работа сил по перемещению пробного заряда по замкнутому контуру не равняется . Это невозможно, поскольку электростатическое поле потенциально. Мы показали, что тангенциальные составляющие напряженности электростатического поля не непрерывны.
Навигация по статьям
