
Статью подготовили специалисты образовательного сервиса Zaochnik.
Пондеромоторные силы в электрическом поле
Содержание:
Напряженность − это основная величина, которая характеризует электрическое поле и вычисляется по формуле:
где − это механическая или пондеромоторная сила, действующая в этой точке поля на пробный заряд . Причем поле образуется всеми зарядами системы, за исключением самого заряда .
Результирующая сила
Большее внимание необходимо уделить вопросу о механических силах, действующих на поверхностные заряды, так как несущая напряженность поля имеет по обе стороны несущей заряд поверхности различные направления и потому на самой поверхности не определена.
Допустим, у нас есть уединенный заряженный проводник, тогда взаимно отталкивающиеся элементы заряда проводника не могут уйти с его поверхности, в результате чего на поверхность проводника действуют пондеромоторные силы, стремящиеся его растянуть. Данные силы оказывают влияние также и на неодиночные проводники в электрическом поле. На элементарный заряд , находящийся на элементе поверхности , действует напряженности поля, которое имеет проводник, поскольку
-я половина создается этим зарядом элемента поверхности. Так, поверхностная плотность такой силы равняется:
где − это поверхностная плотность силы проводника, − это единичный вектор внешней нормали к поверхности проводника, − это диэлектрическая проницаемость среды, с которой соприкасается проводник.
Итак, на поверхности заряженного проводника сила действует в направлении внешней нормали, стремясь увеличить объем тела. Следовательно, результирующую силу можно найти таким образом:
где − это поверхность проводника.
Объемные силы
В диэлектрике объемные электростатические силы, находящиеся в состоянии равновесия, не вызывают движения элементов объема, однако пытаются изменить среду. В итоге появляются объемные силы упругости, уравновешивающие электростатические силы. Только лишь при быстром изменении полей объемные электрические силы вызывают движение элементарных объемов. Применительно к изотропным сжимаемым диэлектрикам с любой зависимостью от плотности массы объемная плотность пондеромоторной силы , которая действует в диэлектрике, помещенном в электрическое поле, равняется:
Если поляризованность линейна к , тогда:
Поверхностные пондеромоторные силы
Кроме объемных сил, в диэлектриках действуют еще и поверхностные пондеромоторные силы.
Допустим, есть плоская граница диэлектриков, параллельная обкладкам конденсатора. Причем напряженность однородного поля перпендикулярна границе диэлектриков. Положительной нормалью будет нормаль, направленная из -й среды во -ю. Тогда поверхностная плотность силы имеет вид:
где − это нормальные составляющие векторов напряженности и электрической индукции. − это диэлектрические проницаемости диэлектриков. Из уравнения понятно, что при На границу раздела диэлектриков сила оказывает в сторону диэлектрика меньшую диэлектрическую проницаемость.
Поверхностная плотность силы
Поверхностная плотность силы состоит из -х частей, а именно:
- Поверхностная плотность силы , действующая на границу раздела диэлектриков и направленная в -ю среду со стороны электрического поля -й среды, которая вычисляется как:
,
где сила направлена по положительной нормали, условно направленной из -ой среды во -ю;
- Плотность силы, действующая на границу против направления положительной нормали со стороны электрического поля -ой среды :
.
В данном случае электрические поля, находящиеся по разным сторонам границы диэлектриков, «притягивают» поверхность раздела с поверхностной плотностью силы, которая равняется объемной плотности электрической энергии, приходящейся на нормальные составляющие векторов поля.
Рассмотрим пример с диэлектриками, плоская граница между которыми находится перпендикулярно обкладкам плоского конденсатора.
Данная поверхностная плотность силы состоит из -х частей, а именно:
- Поверхностная плотность силы , действующая на границу раздела диэлектриков, направленную в -ю среду со стороны электрического поля -й среды, которая вычисляется как:
,
в данном уравнении знак показывает, что сила направлена против положительной нормали, условно направленной из -й среды во -ю;
- Плотность силы, действующая на границу в направлении положительной нормали со стороны электрического поля -й среды
.
Выходит, что электрическое поле «сдавливает» границу раздела благодаря тангенциальной составляющей поля. Поскольку , тогда равнодействующая сил давления равняется:
.
Пондеромоторные силы зачастую находят по связи между энергией электрического поля и силами, действующими на тела в данном поле.
Необходимо получить зависимость пондеромоторной силы, которая действует на диполь в каком-нибудь электрическом поле. При этом напряженность определяется вектором , который может меняться в пространстве. Заряды диполя по модулю равны − это плечо диполя.
Решение
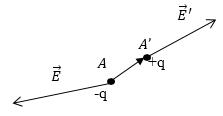
Рисунок 1
Пускай, и − это напряженности поля в точках и , в котором находится диполь
(рисунок ). Вычислим равнодействующую силу , влияющую на диполь:
,
где − это приращение вектора напряженности на отрезке , который равняется длине диполя . Поскольку мало, тогда запишем:
.
Подставив в , получаем:
.
Ответ: Пондеромоторная сила, оказывающая влияние на диполь в электрическом поле, зависит от скорости изменения данного поля в направлении оси диполя: .
Две проводящие плоские пластины составляют угол . Длина пластин, которые расположены перпендикулярно плоскости (рисунок ), бесконечна. Между пластинами постоянная разность потенциалов равняется . Ширина пластины . Пластины не касаются в точке . Краевые эффекты можно опустить. Также можно применить то, что поверхностная плотность заряда пластин заданного конденсатора равняется: , где − это расстояние от оси. Необходимо найти момент силы , который притягивает пластины конденсатора.
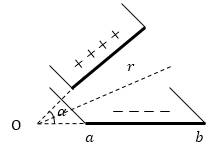
Рисунок
Решение
Поверхностная плотность силы, действующая на проводник, равняется:
.
Получается, что на слой длиной между и действует сила, которая равна:
,
где . Знак показывает, что сила стремится уменьшить угол между пластинами. Вычислим результирующую силу :
.
Линия приложения сил находится на расстоянии от оси вращения. Данное расстояние найдем из условия:
.
Тогда момент силы относительно оси вращения равняется:
.
Ответ: .
Навигация по статьям
