Электроемкость. Конденсаторы

Содержание:

Преподаватель физики

Что такое электроемкость проводников

Если у нас есть два проводника, изолированных друг от друга, которым мы сообщаем некоторые заряды (обозначим их соответственно $q_{1}$ и $q_{2}$ ), то между ними возникнет определенная разность потенциалов. Ее величина будет зависеть от формы проводников, а также от исходных величин зарядов. Обозначим такую разность $Δ φ$ . Если мы говорим о разности, возникающей в электрическом поле между двумя точками, то ее обычно обозначают $U$ .

В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).

Определение 1

Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника $(q)$ к разности потенциалов между этими двумя проводниками.

В виде формулы это записывается так: $C = \frac{q}{∆ φ} = \frac{q}{U}$ .

Для измерения электрической емкости применяется единица, называемая фарад. Она обозначается буквой $Ф$ .

$1 Φ = \frac{1 К л}{1 В}$ .

Конфигурации и размеры проводников, а также свойства диэлектрика определяют величину электроемкости заданной системы. Наибольший интерес для нас представляют проводники особой формы, называемые конденсаторами.

Определение 2

Конденсатор – это проводник, конфигурация которого позволяет локализовать (сосредотачивать) электрическое поле в одной выделенной части пространства. Проводники, составляющие конденсатор, называются обкладками.

Определение 3

Если мы возьмем две плоские пластины из проводящего материала, расположим их на небольшом расстоянии друг от друга и проложим между ними слой диэлектрика, то мы получим простейший конденсатор, называемый плоским. При его работе электрическое поле будет располагаться преимущественно в промежутке между пластинами, но небольшая часть этого поля будет рассеиваться вокруг них.

Определение 4

Часть электрического поля вблизи конденсатора называется полем рассеяния.

Иногда в задачах мы можем не учитывать его и работать только с той частью электрического поля, которое расположено между обкладками. Однако пренебрегать полем рассеяния допустимо далеко не всегда, поскольку это может привести к ошибочным расчетам из-за нарушения потенциального характера электрического поля.

Что такое электроемкость проводников

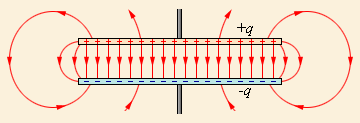
Рисунок $1.6.1 .$ Электрическое поле в плоском конденсаторе.

Что такое электроемкость проводников

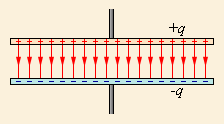
Рисунок $1.6.2 .$ Электрическое поле конденсатора без учета поля рассеяния, не обладающее потенциальностью.

Модуль напряженности электрического поля, которое создает каждая обкладка в плоском конденсаторе, выражается соотношением следующего вида:

$E_{1} = \frac{σ}{2 ε_{0}}$ .

Исходя из принципа суперпозиции, можно утверждать, что напряженность $\vec{E}$ поля, которое создают обе пластины конденсатора, будет равна сумме напряженностей $\vec{E^{+}}$ и $\vec{E^{-}}$ полей каждой пластины, то есть $\vec{E} = \vec{E^{+}} + \vec{E^{-}}$ .

Векторы напряженностей обеих пластин во внутренней части конденсатора будут параллельны друг другу. Значит, мы можем выразить модуль напряженности их суммарного поля в виде формулы $E = 2 E_{1} = \frac{σ}{ε_{0}}$ .

Как рассчитать электроемкость конденсатора

Вне пластин векторы напряженности будут направлены в противоположные друг от друга стороны, значит, $E$ будет равно нулю. Если мы обозначим заряд каждой обкладки как $q$ , а ее площадь как $S$ , то соотношение $\frac{q}{S}$ даст нам представление о поверхностной плотности. Умножив $E$ на расстояние между обкладками $(d)$ , мы получим разность потенциалов между пластинами в однородном электрическом поле. Теперь возьмем оба этих соотношения и выведем из них формулу, по которой может быть рассчитана электрическая емкость конденсатора.

$C = \frac{q}{∆ φ} = \frac{σ \cdot S}{E \cdot d} = \frac{ε_{0} S}{d}$ .

Определение 5

Электрическая емкость плоского конденсатора – величина, обратно пропорциональная расстоянию между обкладками и прямо пропорциональная их площади.

Заполнение пространства между проводниками диэлектрическим материалом может увеличить электроемкость плоского конденсатора в число раз, кратное undefined.

Определение 6

Введем обозначение емкости в виде буквы $С$ и запишем это в виде формулы:

$C = \frac{ε ε_{0} S}{d}$ .

Данная формула называется формулой электроемкости плоского конденсатора.

Конденсаторы бывают не только плоскими. Возможны и другие конфигурации, также обладающие специфическими свойствами.

Определение 7

Сферическим конденсатором называется система из $2$ -х концентрических сфер, сделанных из проводящего материала, радиусы которых равны $R_{1}$ и $R_{2}$ соответственно.

Определение 8

Цилиндрическим конденсатором называется системы из двух проводников цилиндрической формы, длина которых равна $L$ , а радиусы $R_{1}$ и $R_{2}$ .

Обозначим проницаемость диэлектрического материала как ε и запишем формулы, по которым можно найти электрическую емкость конденсаторов:

$C = 4 {πε}_{0} ε \frac{R_{1} R_{2}}{R_{2} - R_{1}}$ (сферический конденсатор),
$C = 2 π ε_{0} ε \frac{L}{\ln \frac{R_{2}}{R_{1}}}$ (цилиндрический конденсатор).

Как рассчитать электроемкость батареи конденсаторов

Определение 9

Если мы соединим несколько проводников между собой, то мы получим конструкцию, называемую батареей.

Способы соединения могут быть разными. Если соединение будет параллельным, то напряжение всех конденсаторов в системе будет одинаково: $U_{1} = U_{2} = U$ , а заряды можно найти по формулам $q_{1} = С_{1} U$ и $q_{2} = C_{2} U$ . При таком соединении вся система может считаться одним конденсатором, электроемкость которого равна $C$ , заряд – $q = q_{1} + q_{2}$ , а напряжение – $U$ . В виде формулы это выглядит так:

$С = \frac{q_{1} + q_{2}}{U}$ или $C = C_{1} + C_{2}$

Определение 10

Если в батарее конденсаторов элементы соединены параллельно, то для нахождения общей электроемкости нам нужно сложить емкости ее отдельных элементов.

Как рассчитать электроемкость батареи конденсаторов

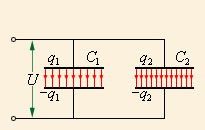
Рисунок $1.6.3 .$ Конденсаторы, соединенные параллельно. $C = C_{1} + C_{2}$

Как рассчитать электроемкость батареи конденсаторов

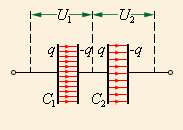
Рисунок $1.6.4 .$ Конденсаторы, соединенные последовательно: $\frac{1}{C} = \frac{1}{C_{1}} + \frac{1}{C_{2}}$

Если же батарея состоит из двух последовательно соединенных конденсаторов, то заряды обоих будут одинаковы: $q_{1} = q_{2} = q$ . Найти их напряжения можно так: $U_{1} = \frac{q}{C_{1}}$ и $U_{2} = \frac{q}{C_{2}}$ . Такую систему тоже можно считать одним конденсатором, заряд которого равен $q$ , а напряжение $U = U_{1} + U_{2}$ .

$C = \frac{q}{U_{1} + U_{2}}$ или $\frac{1}{C} = \frac{1}{C_{1}} + \frac{1}{C_{2}}$

Определение 11

Если конденсаторы в батарее соединены последовательно, то для нахождения общей электроемкости нам нужно сложить величины, обратные емкостям каждого из них.

Справедливость обеих формул, приведенных выше, не зависит от количества конденсаторов в батарее.

Как рассчитать электроемкость батареи конденсаторов

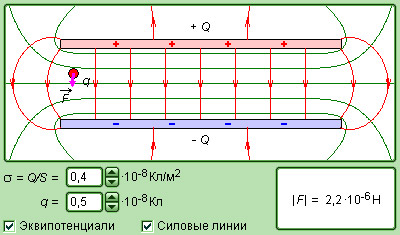
Рисунок $1.6.5 .$ Смоделированное электрическое поле плоского конденсатора.

Курсовая работа по физике

от 5 дней/ от 2160 р.

Реферат по физике

от 1 дня/ от 840 р.

Решение задач по физике

от 1 дня/ от 150 р.